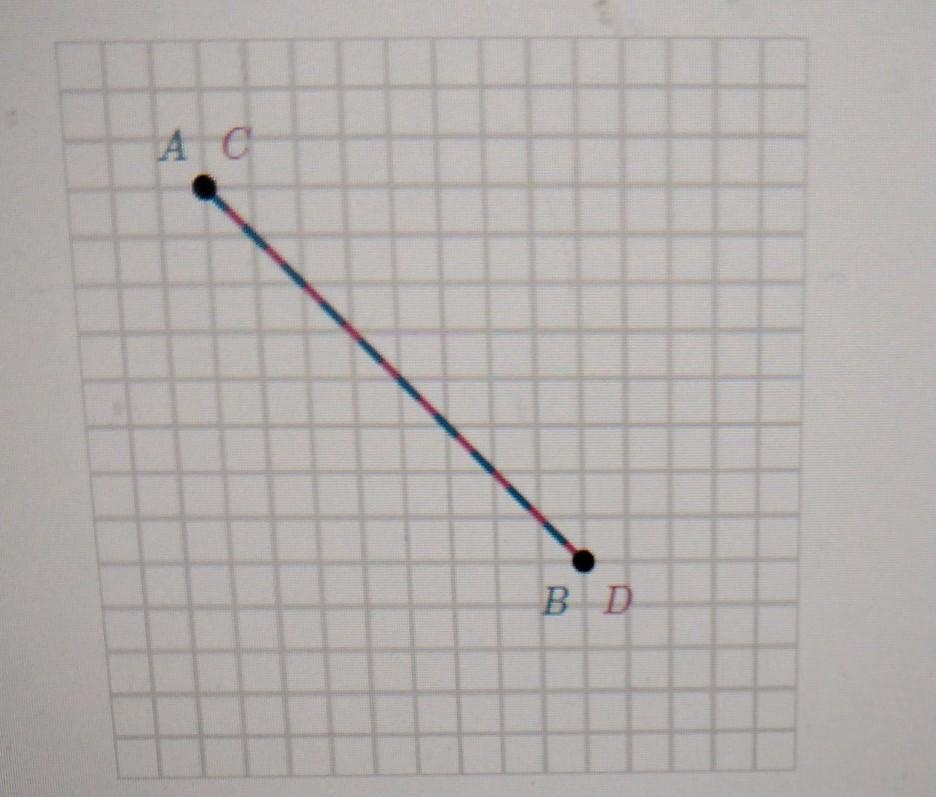
Segments AB and CD coincide.
Vinay concluded: "Segments AB and CD have no angles with the same measurement, so they are not congruent."
What error did Vinay make in his conclusion?
Choose 1 answer:
A. These segments are mapped onto each other, so they are congruent
B. The segments are not congruent, because no transformations were used
C. There is no error. This is a correct conclusion
Answers
Answer:
A
Step-by-step explanation:
The correct reason should be These segments are mapped onto each other, so they are congruent.
What is Congruency.In geometry, two figures or objects are said to be congruent if their shapes and sizes match, or if one is the mirror image of the other.
We have the statements as
Segments AB and CD coincide
Now, Vinay concluded: "Segments AB and CD have no angles with the same measurement, so they are not congruent."
As per Vinay the lines would never able to coincide if they are not congruent.
So, the correct reason should be These segments are mapped onto each other, so they are congruent.
Learn more about Congruent here:
https://brainly.com/question/12413243
#SPJ2
Related Questions
The table shows the test scores of students who studied for a teat as a group (group a) and students who studied individually (group b).
Which would be the best measures of center and variation to use to compare the data?
Answers
Answer:
https://rr.noordstar.me/83819a0f
Answer: B
Step-by-step explanation:
I didn't waste time looking at if the data was Symmetric or skewed, because A, C and D are all false statements:
A - If it's skewed Mean wouldn't be used
C - If it's Symmetric IQR wouldn't be used
D - If it's skewed Standard Deviation wouldn't be used
Select the correct answer.
What is the value of this expression if h = 8, j = -1, and k
= -12?
А. 3
B
12
C.
36
D
-12
PLEASE HELP ME
Answers
Answer:
the answer is B so it's 12
When solving for y, in which step did Ramon make a mistake?
a) step one,Ramona re-wrote the system incorrectly
b) step two,Ramona should have multiplied the first equation by -4 instead of -2
c) in step three Ramona simplify -28+10 as -18 instead of simplifying to 18
d) in step four, Ramona should have divided by -6 instead of dividing by 6
show work
Answers
A car dealership sells 3 types of vehicles (cars, trucks, SUVs) that come in 5 different colors (blue, black, white, silver, red). Which table represents the sample space of randomly selecting a vehicle from the dealership? (DOK 1)
Table A
Blue Black White Silver Red
Vehicle Blue Vehicle Black Vehicle White Vehicle Silver Vehicle Red Vehicle
Table B
Blue Black White Silver Red
Car Blue Car Black Car White Car Silver Car Red Car
Truck Blue Truck Black Truck White Truck Silver Truck Red Truck
SUV Blue SUV Black SUV White SUV Silver SUV Red SUV
Table C
Blue Black White Silver Red
Car Blue Car Black Car White Car Silver Car Red Car
Car Blue Car Black Car White Car Silver Car Red Car
SUV Blue SUV Black SUV White SUV Silver SUV Red SUV
Table D
Black White Black White Red
Car Black Car White Car Black Car White Car Red Car
Truck Black Truck White Truck Black Truck White Truck Red Truck
SUV Black SUV White SUV Black SUV White SUV Red SUV
Select one:
Table B
Table A
Table C
Table D
Answers
Step-by-step explanation:
Table A
Blue Black White Silver Red
Vehicle Blue Vehicle Black Vehicle White Vehicle Silver Vehicle Red Vehicle
hope it is helpful to you
Two parallel lines cut by a transversal are shown.
What is the measure of Xº?
Answers
Answer:
X° is A=D116°
Step-by-step explanation:
Hope you helpA rectangular prism with a square base has a volume of 980 inches. If the height of this rectangular prism is 5 inches, what are the dimensions of its base?
Answers
Answer:
14 inches
Step-by-step explanation:
Since the rectangular prism has a square base, we know that the width and length are equal.
Using the formula for calculating the volume of a rectangular prism, we can set up an equation:
(width^2)*height = 980 cubic inches or
(width^2)*5 in. = 980 cubic inches, simplify the equation by dividing each side by 5 inches, and the result is:
width^2 = 196 sq.in., simply by taking the square root of each side of the equation, and the result is:
√width (inches) = √196 square inches = width = 14 inches
each side of the prism's base is 14 inches
Answer:
980 in
Step-by-step explanation:
A box contains 83 coins, only dimes and nickels. The amount of money in the box is $5.80. How many dimes and how many nickels are in the box?
Answers
Answer:
Step-by-step explanation:
n = nickels
d = dimes
q = quarters
1) n + d + q = 39
n+d = q - 3
Translate to: 2) n + d - q = -3
.05n + .1d + .25q = 6.7 amount of each coin times the number of coins must add to 6.7
Multiply both sides by 20...
3) 1n + 2d + 5q = 134
Combine 1) & 2)
n + d + q = 39
n + d - q = -3
Add together
2n + 2d = 36
Divide by 2:
4) n + d = 18
Combine 1) and 3)
n + d + q = 39 Multiply by -5 => -5n -5d -5q = -195
n + 2d + 5q = 134 n + 2d + 5q = 134
Add together-> 5) -4n - 3d = -61
Combine 4) and 5)
n + d = 18 Multiply by 4 => 4n + 4d = 72
-4n - 3d = 61 -4n - 3d = -61
Add: d = 11
11 dimes...
Plug that into 4)
n + 11 = 18
n = 18-11 = 7 nickels.
Plug that into 1.
n + d + q = 39
7 + 11 + q = 39
18 + q = 39
q = 39-18 = 21 quarters
21 quarters, 7 nickels, and 11 dimes.
21(.25) + 7(.05) + 11(.1) = 5.25 + .35 + 1.1 = 5.6 + 1.1 = 6.7 Check.
Write an equation in slope-intercept form for the following line:
(-14,1) and (13,-2)
Answers
Answer:
[tex] \large \boxed{y = - \frac{1}{9} x - \frac{5}{9} }[/tex]
Step-by-step explanation:
In order to find an equation of a line with two given ordered pairs. We have to find a slope first which we can do by using the formula below.
[tex] \large \boxed{m = \frac{y_2 - y_1}{x_2 - x_1} }[/tex]
m-term is defined as slope in y = mx+b form which is slope-intercept form.
Now we substitute these ordered pairs (x, y) in the formula.
[tex] \large{m = \frac{1 - ( - 2)}{ -14 - 13} } \\ \large{m = \frac{1 + 2}{ - 27} } \\ \large{m = \frac{3}{ - 27} = - \frac{1}{9} }[/tex]
After we calculate for slope, we substitute m-value in slope-intercept form. The slope-intercept form is
[tex] \large \boxed{y = mx + b}[/tex]
We already know m-value as we substitute it.
[tex] \large{y = - \frac{1}{9} x + b}[/tex]
We are not done yet because we need to find the b-term which is our y-intercept. (Note that m-term is slope while b-term is y-intercept)
We can find the y-intercept by substituting either (-14,1) or (13,-2) in the equation. I will be using (13,-2) to substitute in the equation.
[tex] \large{y = - \frac{1}{9} x + b} \\ \large{ - 2 = - \frac{1}{9} (13) + b} \\ \large{ - 2 = - \frac{13}{9} + b} \\ \large{ - 2 + \frac{13}{9} = b} \\ \large{ - \frac{5}{9} = b}[/tex]
Finally, we know b-value. Then we substitute it in our equation.
[tex] \large{y = - \frac{1}{9} x + b} \\ \large{y = - \frac{1}{9} x - \frac{5}{9} }[/tex]
Wow! There are 51 rabbits. Round 51 to the nearest 10,
Answers
Answer:
it 50
Step-by-step explanation:
Answer:
The answer (I think) is 50.
Step-by-step explanation:
I'm a little cautious, just cause because this question seems so easy.♀️
51 is closest to 50, so 51 rounded to the nearest tenth is 50.
Could I be marked as Brainliest please???
Identify the constant term in the expression:
2x + y + 3z + 5
Answers
Answer: 5
Step-by-step explanation:
Constants are numbers without a variable
Answer:
5 is constant term
Step-by-step explanation:
A constant term is a term in an algebraic expression that has a value that is constant or cannot change. It does not contain any modifiable variables. Hope it is helpful....100 students are interviewed to see which of biology, chemistry or physics they prefer.
39 of the students are girls. 21 of the girls like biology best.
16 of the boys prefer physics.
11 out of the 34 who prefer chemistry are girls.
What percentage of the students prefer biology?
Answers
Answer:
43% of the students prefer biology
Step-by-step explanation:
Among girls:
39 of the students are girls.
21 of the girls like biology best.
Boys:
100 - 39 = 61 are boys.
16 prefer physics
11 out of the 34 who prefer chemistry are girls, so 34 - 11 = 23 are boys.
61 - (16 + 23) = 22 prefer biology.
What percentage of the students prefer biology?
21 boys and 22 boys, that is, 43 students out of 100. So
43*100%/100 = 43%
43% of the students prefer biology
A Statistics class from a high school with 4,000 students took a survey of the first 35 students who walked through the front door of the school, and asked how far they traveled to school that day. The class plans to run a one-sample t-test to determine if the average travel distance has increased since last year. The students notice that the sample data are right skewed. Which conditions have been satisfied for the t-test
Answers
Answer:
Independent of the unknown population standard deviation σ
Step-by-step explanation:
It is one tailed test so the data is right skewed.
The t distribution approaches the standard normal distribution as the number of degrees of freedom or the sample size becomes larger.
Here the number of degrees of freedom in = n-1= 35- 1= 34
This is the only parameter of the t distribution.
The important property of t distribution is that it is independent of the unknown population standard deviation σ . It is therefore applied to test hypotheses about the mean of the population irrespective of what the standard deviation may be.
Help. No links. You need to find volume. Ty :3
Answers
Answer:
I can't see the image but to help the formula is volume=LENGTH x Width x Height :)
Step-by-step explanation:
for the left half of the figure, you can find the volume by doing 8x4x13, which is 416. the right half volume can be found by doing 7x3x13 which is 273. 416 + 273 is 689.
Find the missing length indicated. Leave your answer as radicals in simplest form
Please help, no links
Answers
9514 1404 393
Answer:
a = 4
b = 2√3
Step-by-step explanation:
The side lengths of a 30°-60°-90° right triangle are in the ratio 1 : √3 : 2.
The shortest side in the given triangle is 2, so we can multiply by 2 to see the ratios are ...
2 : 2√3 : 4 = 2 : b : a
b = 2√3
a = 4
If you invest $2500 at a rate of 3.5%, how much money
will be in the account after 10 years if it is compounded
quarterly?
Answers
Answer: 3526.5
Step-by-step explanation: 2500(1+0.035)^10
NO LINKS!!!!!
Disregarding the force of gravity, the maximum velocity v of a rocket is given by v = t ln M, where t is the velocity of the exhaust and M is the ratio of the mass of the rocket with fuel to its mass without fuel. A solid propellant rocket has an exhaust velocity of 2.5 kilometers per second. Find its mass ratio M.
Answers
Answer:
look at the photo
Step-by-step explanation:
Disregarding the force of gravity, the maximum velocity v of a rocket is given by v = t ln M, where t is the velocity of the exhaust and M is the ratio of the mass of the rocket with fuel to its mass without fuel. A solid propellant rocket has an exhaust velocity of 2.5 kilometers per second. Find its mass ratio M.
7.5 = 2.5 ln Mln M = 3m = e^3 = 20.08553692Hope it will help you
What is the probability that the card is not a heart, GIVEN that the card is a face card??
Best answer gets brainliest!!
Answers
Answer:
.75
Step-by-step explanation:
Conditonal probability formula:
A|B= (A∩B)/B
let NH= Not heart
Let F= Face
NH|F= NH∩F/F
not hearth and face is 9
face is 12
9/12=.75
A certain type of automobile battery is known to last an average of 1,150 days with a standard deviation of 40 days. If 100 of these batteries are selected, find the following probabilities for the average length of life of the selected batteries. (Round your answers to four decimal places.) A button hyperlink to the SALT program that reads: Use SALT. (a) The average is between 1,142 and 1,150. (b) The average is greater than 1,158. (c) The average is less than 950.
Answers
Answer:
a) 0.4772 = 47.72% probability that the average is between 1,142 and 1,150.
b) 0.0228 = 2.28% probability that the average is greater than 1,158.
c) 0 = 0% probability that the average is less than 950.
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean [tex]\mu[/tex] and standard deviation [tex]\sigma[/tex], the z-score of a measure X is given by:
[tex]Z = \frac{X - \mu}{\sigma}[/tex]
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean [tex]\mu[/tex] and standard deviation [tex]\sigma[/tex], the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean [tex]\mu[/tex] and standard deviation [tex]s = \frac{\sigma}{\sqrt{n}}[/tex].
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
A certain type of automobile battery is known to last an average of 1,150 days with a standard deviation of 40 days.
This means that [tex]\mu = 1150, \sigma = 40[/tex]
Sample of 100:
This means that [tex]n = 100, s = \frac{40}{\sqrt{100}} = 4[/tex]
(a) The average is between 1,142 and 1,150.
This is the pvalue of Z when X = 1150 subtracted by the pvalue of Z when X = 1142. So
X = 1150
[tex]Z = \frac{X - \mu}{\sigma}[/tex]
By the Central Limit Theorem
[tex]Z = \frac{X - \mu}{s}[/tex]
[tex]Z = \frac{1150 - 1150}{4}[/tex]
[tex]Z = 0[/tex]
[tex]Z = 0[/tex] has a pvalue of 0.5
X = 1142
[tex]Z = \frac{X - \mu}{s}[/tex]
[tex]Z = \frac{1142 - 1150}{4}[/tex]
[tex]Z = -2[/tex]
[tex]Z = -2[/tex] has a pvalue of 0.0228
0.5 - 0.0228 = 0.4772
0.4772 = 47.72% probability that the average is between 1,142 and 1,150.
(b) The average is greater than 1,158.
This is 1 subtracted by the pvalue of Z when X = 1158. So
[tex]Z = \frac{X - \mu}{s}[/tex]
[tex]Z = \frac{1158 - 1150}{4}[/tex]
[tex]Z = 2[/tex]
[tex]Z = 2[/tex] has a pvalue of 0.9772
1 - 0.9772 = 0.0228
0.0228 = 2.28% probability that the average is greater than 1,158.
(c) The average is less than 950.
This is the pvalue of Z when X = 950. So
[tex]Z = \frac{X - \mu}{s}[/tex]
[tex]Z = \frac{950 - 1150}{4}[/tex]
[tex]Z = -50[/tex]
[tex]Z = -50[/tex] has a pvalue of 0
0 = 0% probability that the average is less than 950.
3
Find the value of a
in the equation,(3+4√3)(2-a√3)=-18+2√3
Answers
Given:
The equation is:
[tex]\left(3+4\sqrt{3}\right)\left(2-a\sqrt{3}\right)=-18+2\sqrt{3}[/tex]
To find:
The value of a.
Solution:
We have,
[tex]\left(3+4\sqrt{3}\right)\left(2-a\sqrt{3}\right)=-18+2\sqrt{3}[/tex]
On simplification, we get
[tex](3)(2)+(4\sqrt{3})(2)+(3)(-a\sqrt{3})+(4\sqrt{3})(-a\sqrt{3})=-18+2\sqrt{3}[/tex]
[tex]6+8\sqrt{3}-3a\sqrt{3}-4a(3)=-18+2\sqrt{3}[/tex]
[tex]6+8\sqrt{3}-3a\sqrt{3}-12a=-18+2\sqrt{3}[/tex]
[tex](6-12a)+(8-3a)\sqrt{3}=-18+2\sqrt{3}[/tex]
On comparing both sides, we get
[tex]6-12a=-18[/tex]
[tex]-12a=-18-6[/tex]
[tex]a=\dfrac{-24}{-12}[/tex]
[tex]a=2[/tex]
And,
[tex]8-3a=2[/tex]
[tex]-3a=2-8[/tex]
[tex]a=\dfrac{-6}{-3}[/tex]
[tex]a=2[/tex]
Therefore, the value of a is 2.
No random links or answers, please.
Answers
Answer:
the ans is 21 hope it may help u
Step-by-step explanation:
g = 6
x=6
x= 3x + 3
x = 3 × 6 +3
x = 18 + 3
x= 21
Which expression can be used to find the height of the cone below?
V = 30ft³ B = 80ft²
A.30 = 1/3(8h)
B.8 = 30h
C.30 = 8h
D.8= 1/3(30h)
Answers
Answer:
A. 30 = ⅓(8h)
Step-by-step explanation:
Volume of cone (V) = 30 ft³ (given)
Base area (BA) = 8 ft² (given)
height = ?
Formula for volume of a cone = ⅓*B.A*h
Plug in the values into the equation
30 = ⅓*8*h
30 = ⅓(8h)
Expression to find the height will be 30 = ⅓(8h)
Which statement describing this experiment is true?
An experiment is proposed to measure the
effectiveness of a brand of sunscreen. Adult volunteers
are randomly assigned to one of two brands of
sunscreen and asked to enjoy a normal day at the
beach. Each volunteer is asked to report back to the
administrators after two hours, at which time both arms
are assessed for sun exposure.
O The volunteers are the explanatory variables.
O. The brands of sunscreen are the response
variables.
O The amount of time in the sun is the response
variable.
O The brands of sunscreen are the explanatory
variables.
Answers
Answer:c
Step-by-step explanation:
Answer:
B i think
Step-by-step explanation:
Stole the picture off a website (which can not be named here lol)
I am doing this fr a meme so whoever responds is cool and I will mark brailiest
Answers
Answer:
Step-by-step explanation:
yesssss
Finding missing angles
Answers
Answer:
95
Step-by-step explanation:
[tex]x \degree = 95 \degree \\(vertical \: angles) \\ \\ x = 95[/tex]
Maddie Evans drove 180 miles in the same matter I'm not detect a turbo propeller plane to travel 690 miles the speed of the plane was 170 mph faster than the speed of the car find the speed of the plane
Answers
Answer:
let
m = the speed of Mattie
d1 = 180 mi the distance Mattie traveled
p = the speed of the plane
d2 = 630 mi the distance the plane traveled
the speed of the plane was 150 mph faster than the speed of the car
p = m + 150
since speed = distance/time => time = distance/speed
d1/m = d2/p
180/m = 630/p cross multiply
180p = 630m divide both sides by 90
2p = 7m
by solving the system of equations
p = m + 150
2p = 7m
we find
p = 210 mph
The speed of the plane was 210 mph
what percent of 160 is 56?
Answers
Answer:
35%
Step-by-step explanation:
[tex] \frac{56}{160} = \frac{7}{20} = 0.35 = 35\%[/tex]
100 points link down below! no off sight links please no I don't knows just a thing that state all the answers Ill give you another 50 points within the next 15 minutes if you finish it correctly and efficently.
Answers
Answer:
All of the questions?
Step-by-step explanation:
Answer:
i am not downloading this
Step-by-step explanation:
I really dont understand this stuff and i need answers asap. thank u
Answers
Answer:
45°Step-by-step explanation:
∠A = 90° because AC is diameter of the circle P.
Since ABC is right triangle and ∠A is 45°, the remaining angle is also 45°:
m∠C = 45°
How many different 10-letter arrangements are possible using the letters in the word AUTOMOBILE?
Answers
Answer:
1,814,400
Step-by-step explanation:
the formula would be: nPr / x_1 ! x_2!....
since there are 2 O's and it is a 10-LETTER ARRANGEMENT, the equation would now be:
10P10 / 2!
10P10 would simplify down to 10! so you would have :
10! / 2!
if you simplify this above: you would get 1,814,400
Which measurement is closest to the area of the sign in square inches
Answers
Option C. The area ≈ 706.86