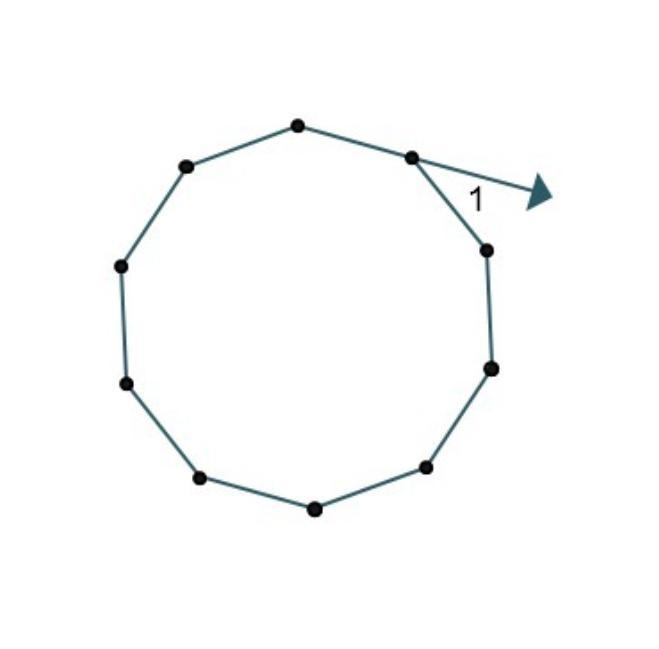
5. In the regular decagon shown, what is the measure of angle 1? *
1 point
One Exterior Angle of a REGULAR Polygon
OneEx 4 = 360
(
18 degrees
O
36 degrees
72 degrees
0
180 degrees
Answers
The image of the hexagon is missing, so i have attached it.
Answer:
∠1 = 36°
Step-by-step explanation:
From the image attached, we can see that the polygon is regular and has 10 sides.
Formula for an interior angle of a regular polygon is;
θ = 180(n - 2)/n
Where n is the number of sides of the polygon.
Thus;
θ = 180(10 - 2)/10
θ = 144°
Now, ∠1 forms a straight line with one of the interior angles of the polygon.
Thus, θ + ∠1 will be equal to 180° because sum of angle on a straight line is 180°
Thus;
144° + ∠1 = 180°
∠1 = 180° - 144°
∠1 = 36°
Related Questions
Consider the geometric sequence 8,4,2,1,...
Answers
Answer:
Its A for the function that represents the geomertric sequence
Given b=4, c=1, A=120° for a triangle with sides a, b, c and angles A, B, C. What is the area of the triangle? Round to the nearest hundredth.
Answers
Answer:
1.73 units
Step-by-step explanation:
The area of a triangle with sides a, b, c and angles A, B, C is given as
Area = 1/2 bc sin A
Given that b=4, c=1, A=120° for a triangle with sides a, b, c and angles A, B, C then the area
= 1/2 * 4 * 1 * sin 120
= 2 sin 120
= 2 * √3/2
= √3
= 1.732
To the nearest hundredth = 1.73